When creating an investment plan, look no further than dividend stocks for retirement. Dividend stocks can provide a great way to build up retirement income. In fact, when markets are topsy-turvy, and the economic future is uncertain, one of the best things to own are dividend stocks.
If you’re still in the accumulation phase, you might want to favor growth-oriented stocks. But retirees are more often in the preservation phase, and there is a strong urban myth that they should rely heavily on bond interest payments for their retirement income. We respectfully disagree.
Historically, bonds do not keep pace with inflation, and this urban myth can seriously compromise your retirement planning. Bonds still have a role to play, but the old guidelines emphasizing bonds in a retirement portfolio are outdated. To achieve their retirement dreams, the vast majority of retirees need to own a healthy allocation of stocks and specifically look to include dividend stocks in that portfolio.
Why Dividend Stocks
Dividend stocks are stocks that specifically pay income to the owner. Not all stocks do that, nor do they necessarily need to. Owning stock means you own a share of a publicly-traded company. It also means you own a share of that company’s profits. You, along with other shareholders, employ managers who are responsible for determining how to generate and use those profits.
Companies focused on growing quickly will usually retain profits to purchase new equipment, build new factories, etc. Companies that are in older, more mature industries typically don’t have to use all their profits to fuel growth. They can return some of those profits each year to the shareholders. Dividends are the portion of the profits that management has decided to pay to shareholders.
Stock dividends are like bond interest income in the sense that you receive cash income from your investment. Right now, the average dividend yield for the S&P 500 companies is 1.80%. That’s already better than the 30-year treasury. But wait, the S&P 500 includes both “growth” and “value” oriented companies. If we look at value-oriented companies, which typically pay greater dividends, the average yield today is 2.83%, as measured by the S&P 500 value index.
Dividend stocks are great for retirement income because they tend to pay consistent income and provide an opportunity to grow in value. Typically, bonds will not increase in value. If you buy a $100,000 bond today and hold it until it matures, you can expect to be repaid $100,000. If you buy $100,000 in value stocks (using their 15-year history as a guide), they would be worth roughly $180,000 in 15 years. That’s why retirees should own a healthy portion of dividend stocks in retirement.
But Aren’t Stocks Generally Riskier Than Bonds?
Another urban myth is that stocks – even the best dividend stocks – are always riskier than bonds. That’s simply not true. Research by Fidelity going back to 1926 has shown that “equities are less volatile than bonds in the long term.”
Of course, the “long-term” may be longer than many people have patience for, so this is an academic exercise at some level. The wisest course of action is to acknowledge that ALL investments have their own volatility. The important question to ask is how you can diversify among the various investments to mitigate overall volatility. Dividend stocks should have a core weighting in almost every portfolio, but not because they are more or less volatile than something else.
Once that allocation decision is made, then you can enjoy one of the key benefits of dividend stocks; the fact that many of them, particularly blue chip stocks, increase their dividends over time. This helps tremendously in overcoming the negative impact inflation can have on your potential retirement income.
Dividend Growth
Dividend growth is one of the great advantages available to stock investors. Companies that pay dividends have a built-in incentive to keep paying the dividend and to increase it over time. The reason is simple; any company which generates consistent profits that allow the company to pay cash dividends to their shareholders and to increase those dividend levels is a company that is doing well. It’s not a guarantee – management and markets can change – but it’s a pretty good indicator. Company management wants to keep shareholders happy and supply evidence they’re doing a good job. So typically, stock dividends tend to grow over time, unlike the interest from bonds.
The bond interest rate is determined when the bond is issued. The original owner, and any future owner of that bond, should receive the same interest no matter how long the bond has until maturity. The company or government agency that issued the bond does not have any incentive to increase interest payments over time, nor does the bond’s legal structure even allow this type of latitude. Once the bond is issued, the interest rate formula is set. That’s one of the main reasons why stocks should be a part of every investor’s portfolio; dividends can grow over time, and it bears repeating that dividend growth has historically been greater than inflation.
Dividend growth also provides an opportunity to use a smart strategy for investors to amplify returns: use those dividends to reinvest in the stock. Following this strategy means that each dividend payment will result in you owning more of the company which pays the dividend. If you select the right dividend stocks for retirement income, you will earn a rate of return from the dividends, you will earn a rate of return from the increases in the dividends over time, and you will earn a rate of return from the increasing number of shares you’ll own over time
Dividend Growth Example
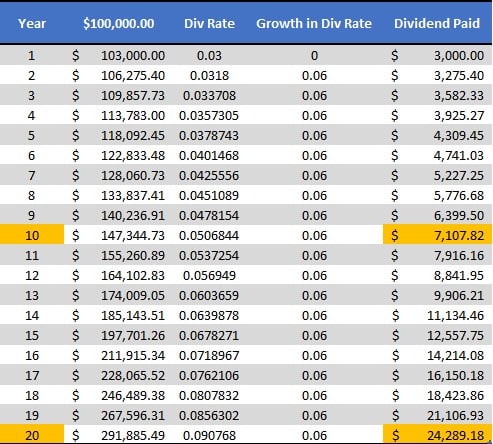
Just to cement this in, let’s look at an example. Assume you bought 1,000 shares of a stock trading at $100/share. That would represent a total investment of $100,000. If the stock has a 3% dividend yield, you will receive a dividend of $3 per share in the course of a year. That’s $3,000 in dividends. If you take that $3,000 and reinvest it, you would own $103,000 of the stock. If this company’s management decides to increase its dividend by 6%, you will receive a dividend the next year of 3.18%. Because you own more shares, that 3.18% dividend on your investment would generate a $3,275 dividend. We realize there’s a lot of math here, but this means that the rate of return on your original investment would be 3.28%, and that assumes the stock price hasn’t increased.
This dividend reinvestment strategy continues to increase the return on your original investment over time. After 10 years, this hypothetical investment would produce roughly $7,108 in dividends; after 20 years, you would receive more than $24,289 a year in dividends.
Which Dividend Stocks Are Best For Retirement Income?
If you’re ready to find the best dividend stocks for retirement income right now, watch out. One of the temptations of investing is that once you learn about a good strategy, you convince yourself you can do it as well as a professional can.
Hopefully, by phrasing it in that way, the answer becomes obvious. Just asking yourself whether you can do something can lead to a positive answer – “sure, I can do that.” – but it may well be the wrong answer relative to what you’re trying to achieve.
As an example, I can do plumbing. But I’m not very good at it. If I want a so-so job at my house, I’ll do the plumbing, but I’ve acknowledged that it won’t be as good a job as if I hired a professional to do it. So, outside plumbing, like replacing a hose bib? Sure, I’ll do that. But the minute I step across the threshold into the house, I know that my work on the sink will not look (and might not work) the way we want it to.
We all have these areas. You might be great at plumbing, and you’re to be commended. The last time I tried that (when I learned I didn’t have the skill), I almost swamped a bathroom. You have to know where you’re good and where you’re not. Most people don’t have careers in investment management. Acknowledging that, why would anyone conclude that they should still attempt to enter this market and compete with the professionals?
And the fact that there is competition is one of the keys to determining success or failure. Just buying a dividend stock does not guarantee you success in achieving your financial goals. Moreover, all stocks, including dividend stocks, can be overpriced, underpriced, or correctly priced. Buying too high will reduce the benefit of owning a dividend stock. Buying at a discount will amplify the benefit of owning a dividend stock.
Good Stocks Don’t Always Remain Good
Furthermore, “good” stocks don’t always remain “good.” Company management changes, industries change, the competitive landscape changes, and a well managed successful company may become poorly managed and unsuccessful. Sears is a perfect example; once the retail category leader, its market changed, its management became complacent – some argue they became arrogant – and they spiraled downward.
Let’s look at a couple of examples to see how this plays out. Suppose you have an acquaintance who wants to sell you a dividend stock and suppose that stock pays a dividend of 4%. What if the price your friend wants for the stock is 3% too high? If you buy it, you’ll receive the 4% dividend that year, but you’ll see the price fall by 3%. Your total return will be 1% because you purchased the stock at too high a price.
Alternately, let’s say you purchased Sears at the “right” price back in 1980 because it had a great dividend yield (it was paying 4.7% per year). As we summarized above, Sears lost its grip on its customers and went from a leader to a laggard. Holding Sears during its descent would have lost money despite its 4.7% yield.
Good dividend stocks are good stocks, and bad dividend stocks are bad stocks. In fact, this is true for any investment category. We could say the same thing about growth stocks, small cap stocks, or international stocks. The point is knowing which dividend stocks are best for retirement, at what price you should buy them, and at what price you should sell them. The decisions which need to be made are much easier to list than to practice. The investment world is full of professional money managers whose job is to know their market segment and understand the companies they are analyzing to make these decisions correctly day in and day out.
Leave It To The Professionals
An individual investor who believes he or she can make these decisions, as well as a good professional, is deluded. Investment managers specialize, and the best ones stick to their specialty. The value manager focuses on value stocks; the growth manager focuses on growth stocks; the small cap manager focuses on small cap stocks. You get the picture. They do this because it takes everything they’ve got to eat, breathe, and sleep in their area of specialty to compete with all the other managers in their specialty to purchase the right stock at the right price. As our illustrations above demonstrated, buying the wrong stock or buying the right stock at the wrong price will determine success or failure.
To compete as an amateur against professional dividend stock managers to buy the correct stocks at the correct prices – and then sell them later at the correct price – is a recipe for sub-par performance and perhaps even substantial losses in your portfolio.
To quote one of those ubiquitous television car commercials we’ve all seen, “these are trained professionals on a closed track; don’t try this at home.”
Use Professional Money Managers to Invest in Dividend Stocks for Retirement
The good news is that professional investment management is available to almost anyone. Professional money managers typically work for investment fund companies. There are hundreds of substantial investment fund companies in the US, collectively offering more than 9,500 funds encompassing all types of stocks and bonds, including dividend stocks.
There are open-end funds, closed-end funds, active managers, passive managers, iShares, and ETFs. Each one of them is managed by a professional money manager or team of professional money managers. This is how to invest in dividend stocks; pick a dividend stock fund and let the manager’s skill, experience, and knowledge work for you rather than against you. You do not want to compete against these guys or gals to purchase the limited number of dividend stocks available at the right price and the right time.
Thinking About Dividend-Focused Mutual Funds or ETFs? Watch Out For Fees
Hopefully, you’re thinking, “I like this dividend stock strategy, but instead of trying to compete against the pros, I’ll join with the pros by buying a dividend-focused mutual fund or ETF.” While there is a lot to wisdom to this approach, be aware that some mutual funds and specialized ETFs carry high fees, which may reduce your dividend gains or income, and some of these funds aren’t that good.
We wish we could say that all professional managers are good (just because they are professional), but that would be as misleading as saying that all doctors are the same (just because they all have graduated medical school). Years of training, experience, and intelligence do not guarantee success.
This doesn’t invalidate the strategy of using dividend stocks or of harnessing the power of professional managers any more than the existence of a bad doctor invalidates the wisdom of using a good doctor. It simply means that implementing the strategy requires a bit more work than thumbing through the yellow pages or the digital pages of mutual fund directory.
You need to weed out the bad managers, and even the “lucky” managers, from the truly good ones. Here’s where an objective investment consultant can help you. Don’t trust an advisor who is paid a commission by the mutual fund company; that person is a “sales rep,” not an “objective advisor.” Fiduciary advisors are at the top of the quality pyramid and offer 100% objective advice. They typically have the experience and research tools to determine which dividend stock fund or ETF is best for you.
Dividend Stock Income is Just One Aspect of Planning For a Comfortable Retirement
Stocks are typically an excellent investment for many people, and dividend stocks can be especially helpful in generating retirement income. But it is just one aspect of achieving a comfortable retirement. As we’ve mentioned above, stocks AND bonds both are volatile. Every investment category has its own volatility.
Determining how much volatility is right for you at this stage of your life is important. The allocation between stocks and bonds will allow you to mitigate that volatility. But this takes a bit of analysis to get right. We have a short investment risk tolerance questionnaire that will help you better understand the tradeoffs and frame the conversation in a helpful way.
Get Professional Advice
Retirement income planning is critically important, but it’s not necessarily that easy. In fact, it can be pretty tricky to do yourself. There are many moving pieces, and how much you allocate to stocks and which dividend stocks you use are only part of the equation. The quiz referenced above will provide a framework to analyze your unique situation further and to develop specific solutions that are right for you.
There shouldn’t be anything cookie-cutter about your retirement plan; it’s too important to simply rely on the online calculators, and canned software approaches so many sales reps (sometimes claiming to offer advice) use. Their goal is to get you to the buying decision as quickly as possible, and too often, what you’re buying will do more harm than good.
We’d love to chat with you in greater detail about your unique situation and needs. We don’t use sales tactics, don’t sell products or take commissions, and we NEVER compromise our objectivity and dedication to helping you achieve your goals. If you’d like to schedule a complimentary initial consultation with a fiduciary advisor, please click the link below and begin the journey to a successful retirement.
Greg Welborn is a Principal at First Financial Consulting. He has more than 35 years’ experience in providing 100% objective advice, always focusing on the client’s best interests.
Greg Welborn is a Principal at First Financial Consulting. He has more than 35 years’ experience in providing 100% objective advice, always focusing on the client’s best interests.